Pendel Programmieren - Akademie Tutorium Berlin

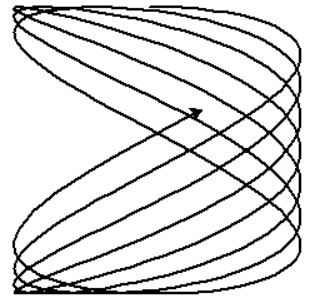
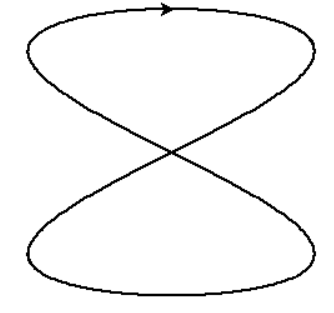
Ich habe ein Code in „Python“ geschrieben bei dem ein Pendel simuliert wird. Gezeichnet wird der Pfad über der Ebene/Untergrund. Du kannst nun angeben wie oft es je in beide Bewegungs-Richtungen komplett einmal schwingt (hin und her).

Dadurch ergeben sich wunderbaremuster probiert es gerne mal aus.

Viel Spaß. Wenn Du Fragen oder Hinweise dazu hast, schreibe mir auch gerne eine Mail an: gabriel@akademie.tutorium-berlin.de oder Mind-Life@gmx.de

2. Version:

Download: 1PendelKar2.py

Diese Version arbeitet mit dem kartesisches Koordinaten.

1. Version:

Download: 1PendelPolarl2.py

Diese Version arbeitet mit dem polaren Koordinaten.

———————————————————-

1PendelKar2.py #Bibliotheken
import turtle as trl
import numpy as np
print(„\nSimulation eines Pendels das über einer Ebene schwingt. \n“
„Gezeichnet wird der Pfad über dieser. Du kannst nun angeben wie oft es\n“
„je in beide Bewegungs-Richtungen komplett einmal schwingt (hin und her).\n“
„Viel Spaß dabei.\n“
„Nur ganze positive Zahlen: (Beispiele: 5 und 3, 7 und 13, 1 und 2)\n“) #Input
p1 = int(input(„Schwingungsanzahl 1.Achse: „))
p2 = int(input(„Schwingungsanzahl 2.Achse: „)) #Häufigste Schwingung auf der X-Achse
if p1 < p2:
p1, p2 = p2, p1 #Skalierung
sk = 100 #Startpunkt
wri = 0
trl.up()
trl.goto(0,sk)
trl.down()
trl.width(2) #Laufende Berechnungen
for i in range(361): x = np.sin(p1*wri) * sk
y = np.cos(p2*wri) * sk

trl.goto(x,y)
wri = wri + np.pi/180

trl.done()

1PendelPolarl2.py #Bibliotheken
import turtle
import numpy as np #Standartwerte + Start-Flag
global winkelgradI
winkelgradI = 0
global z
z = 0 #Umwandlung zwischen kartesisches und polarem Koordinatensystem
def cart2pol(x, y):
global rho, phi
rho = np.sqrt(x**2 + y**2)
phi = np.arctan2(y, x)
return(rho, phi)
def pol2cart(rho, phi):
global x,y
x = rho * np.cos(phi)
y = rho * np.sin(phi)
return(x, y)

print(„\nSimulation eines Pendels das über einer Ebene schwingt. \n“
„Gezeichnet wird der Pfad über dieser. Du kannst nun angeben wie oft es\n“
„je in beide Bewegungs-Richtungen komplett einmal schwingt (hin und her).\n“
„Viel Spaß dabei.\n“
„Nur ganze positive Zahlen: (Beispiele: 5 und 3, 7 und 13, 1 und 2)\n“) #Input
p1 = int(input(„Schwingungsanzahl 1.Achse: „))
p2 = int(input(„Schwingungsanzahl 2.Achse: „)) #ÄNDERE HIER zum Drehen der Zeichnung in Grad 0°-360° ohne °
turtle.right(0) turtle.up()
turtle.goto(0,100)
turtle.down() #ÄNDERE HIER um die Farbe und die Dicke der Linie anzupassen
turtle.color(„black“)
turtle.width(2) #Laufende Berechnungen
for i in range(721):

winkelradi = np.radians(winkelgradI) if p1 > p2:
p1, p2 = p2, p1 #Vertauschen der Werte vektorX = p1*np.sin(p1*winkelradi)
vektorY = p2*np.cos(p2*winkelradi)

cart2pol(vektorX, vektorY) #Umrechnung von -180 bis 180 zu einem 360° Voll-Kreis Winkel
if phi < 0:
phi360 = phi + 2*np.pi
elif phi >= 0:
phi360 = phi #Erster Schritt(einmalig) mit Anfangswinkel also 0° Korrektur
zwaN1 = np.degrees(phi360)
if z == 0:
zwaN = zwaN1
z = 1

#zwaN1 = Alter Zeichen Winkel
#zwaN1 = Neuer Zeichen Winkel
#zwaK = Korrektur Zeichen Winkel
zwaK = zwaN1-zwaN

# Für Drehungen über die 360°/0° Achse
if zwaK > 180:
zwaK = -(360 – zwaN1 + zwaN) elif zwaK < -180:
zwaK = 360 – zwaN + zwaN1

#Zeichnung
turtle.speed(5) #ÄNDERE HIER die Zeichengeschwindigkeit von 1-10
turtle.left(zwaK)
turtle.forward(rho*1) #ÄNDERE HIER den Faktor *1 um die Größe des Schwingens zu ändern „““ Möglichkeit zum Anzeigen einiger Laufenden Werte
print(winkelgradI)
print(rho, phi)
print(zwaN,zwaN1, zwaK)
print(‚IIIIIIIIIIIIIIIIIIIIIIIIIIIIII‘)“““

zwaN = zwaN1
winkelgradI = winkelgradI + 0.5

turtle.done()